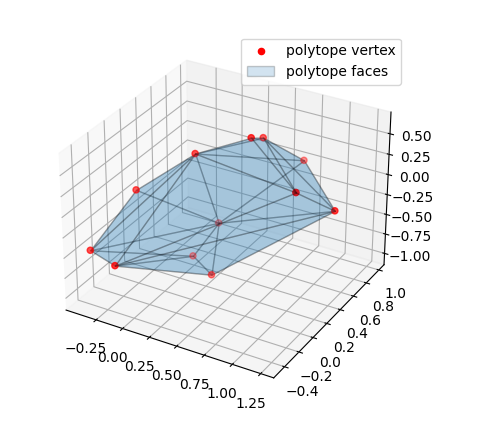
Find a vertex representation of a set of half-planes

A simple example program for find a vertex representation of a set of half-plane \(Àx\leq b\)

from pycapacity.objects import Polytope # import polytope object
import numpy as np

N = 100 # hundred inequalities (half planes)
m = 3   # space dimension

# this seed is used to generate the same image
# as in the examples in the docs
np.random.seed(12345)

# define the inequalities
A = np.random.rand(N,m)*10-5
b = np.random.rand(N)*50

# generate the polytope object
p = Polytope(H=A,d=b)
# find the vertices
p.find_vertices()

# print the vertices number
print('Number of vertices found: ', p.vertices.shape[1])


# visualise the polytope found
# plotting the polytope
import matplotlib.pyplot as plt
from pycapacity.visual import *
fig = plt.figure(4)

# draw faces and vertices
plot_polytope(plot=plt,
                polytope=p,
                label='polytope',
                edge_color='black',
                vertex_color='red',
                alpha=0.2)

plt.legend()
plt.show()

The output of this program will be an image visualised vertices and faces of the specified inequalities \(Àx\leq b\)

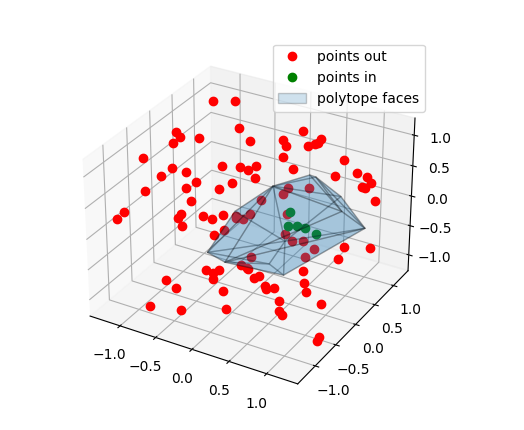
Classify points in or out the polytope

# generate points to classify
points_to_classify = np.array(np.random.rand(m,N))*2.5-1.25 # points

# classify the points
points_in, points_out = [], []
for point in points_to_classify.T:
    if np.all(A@point <= b):
        points_in.append(point)
    else:
        points_out.append(point)
points_in = np.array(points_in).T
points_out = np.array(points_out).T

# plotting the polytope and the points
fig = plt.figure(5)

# draw faces and vertices
plot_polytope(plot=plt,
                polytope=p,
                label='polytope',
                edge_color='black',
                show_vertices=False,
                alpha=0.2)
# points out in red
plt.plot(points_out[0,:],points_out[1,:],points_out[2,:],'ro',label='points out')
# point in in green
plt.plot(points_in[0,:],points_in[1,:],points_in[2,:],'go',label='points in')
plt.legend()
plt.show()

The output of this program will be an image of visualised classified points in or out the inequalities \(Àx\leq b\)