About pycapacity
An efficient task-space capacity calculation package for robotics and biomechanics
Note
pycapacity package is out- version v2.1! - see full changelog

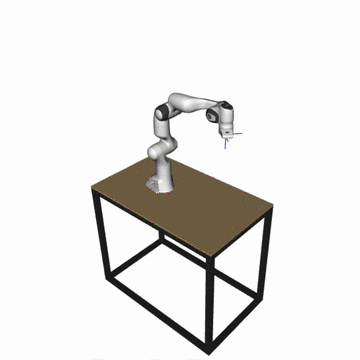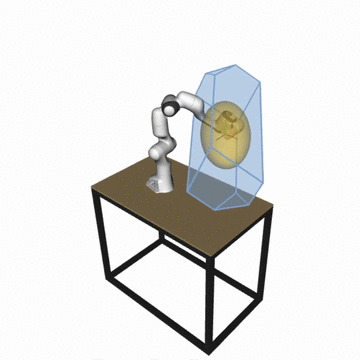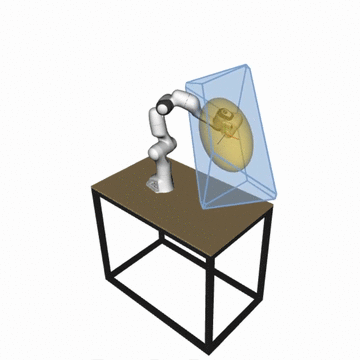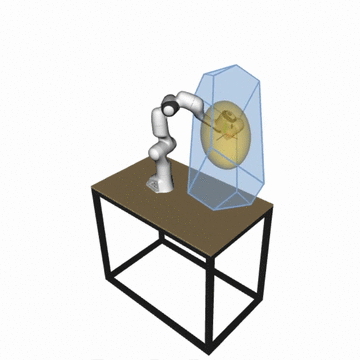

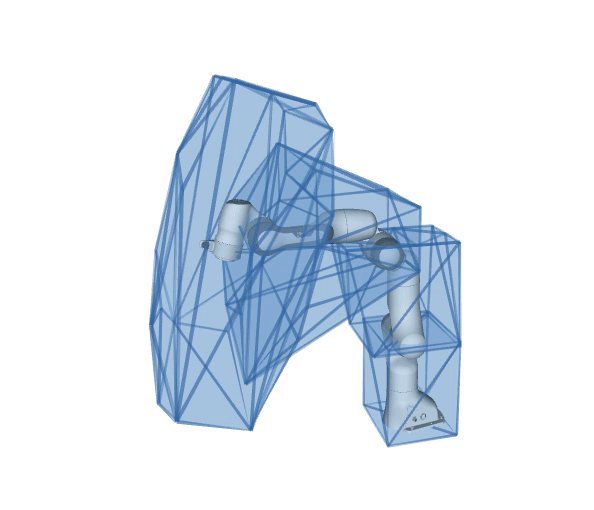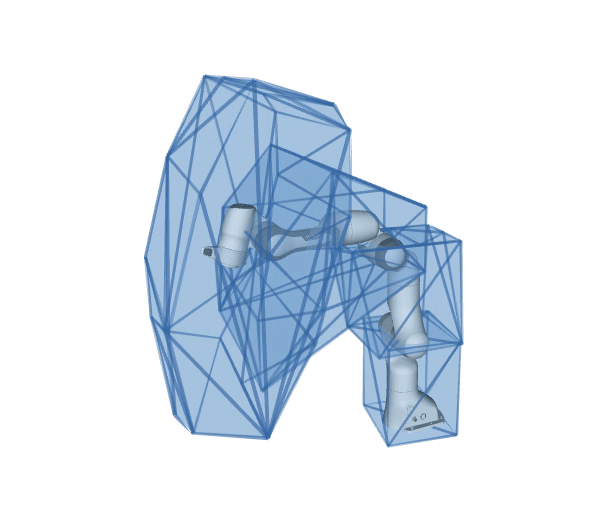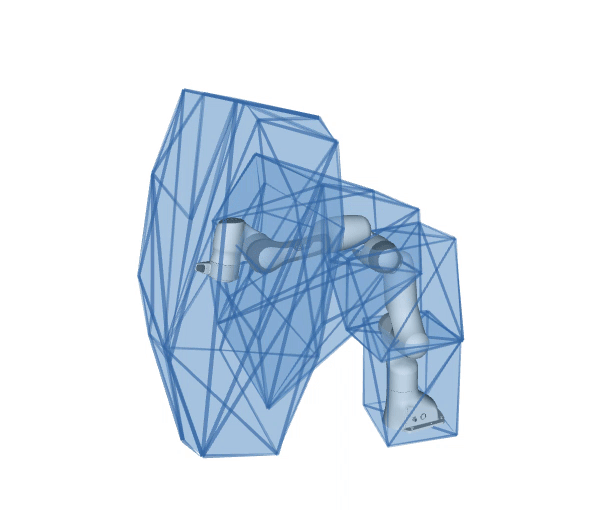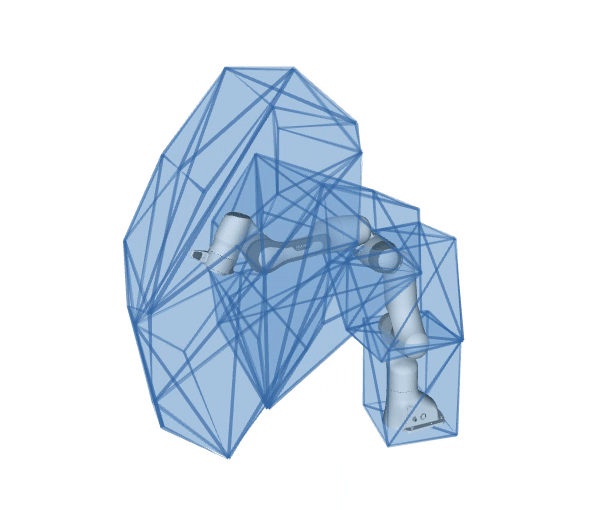
What is pycapacity?
Python package pycapacity provides a set of tools for evaluating task space physical ability metrics for humans and robots, based on polytopes and ellipsoids.
The aim of pycapacity is to provide a set of efficient tools for their evaluation in an easy to use framework that can be easily integrated with standard robotics
and biomechanics libraries. The package implements several state of the art algorithms for polytope evaluation that bring many of the
polytope metrics to the few milliseconds evaluation time, making it possible to use them in online and interactive applications.
The package can be easily interfaced with standard libraries for robotic manipulator rigid body simulation such as robotic-toolbox
or pinocchio, as well as human musculoskeletal model biomechanics
softwares opensim and biorbd. The package can also be used with the Robot Operating System (ROS).
The package additionally implements a set of visualization tools for polytopes and ellipsoids based on the
Python package matplotlib intended for fast prototyping and quick and interactive visualization.
Implemented metrics
This package implements polytope and ellipsoid based physical ability metrics for robotic manipulators and human musculoskeletal models.
Robotic manipulator capacity metrics
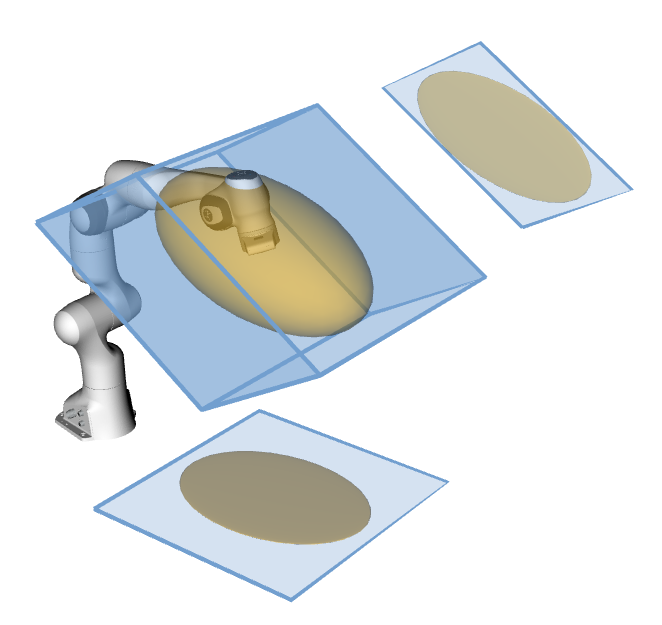
For the robotic manipulators the package integrates several velocity, force and acceleration capacity calculation functions based on ellipsoids:
Velocity (manipulability) ellipsoid
\[E_{v} = \{\dot{x} ~| \dot{x} = J\dot{q},~ ||W^{-1}\dot{q}||\leq1 \}, \qquad W = diag(\dot{q}_{max})\]Acceleration (dynamic manipulability) ellipsoid
\[E_{a} = \{\ddot{x} ~| \ddot{x} = JM^{-1}\tau,~ ||W^{-1}\tau||\leq1 \}, \qquad W = diag(\tau_{max})\]Force ellipsoid
\[E_{f} = \{{f} ~| J^{T}f = \tau,~ ||W^{-1}\tau||\leq1 \}, \qquad W = diag(\tau_{max})\]
And polytopes:
Velocity polytope
\[P_{v} = \{\dot{x} ~| \dot{x} = J\dot{q},~ \dot{q}_{min}\leq\dot{q}\leq\dot{q}_{max} \}\]Acceleration polytope
\[P_{a} = \{\ddot{x} ~| \ddot{x} = JM^{-1}\tau,~ \tau_{min}\leq\tau\leq\tau_{max} \}\]Force polytope
\[P_{f} = \{f ~| J^{T}f = \tau,~ \tau_{min}\leq\tau\leq\tau_{max} \}\]Force polytopes Minkowski sum and intersection
\[P_{\cap} = \mathcal{P}_{f1} \cap \mathcal{P}_{f1} \qquad P_{\oplus} = \mathcal{P}_{f1} \oplus \mathcal{P}_{f1}\]
Where \(J\) is the robot jacobian matrix, \(f\) is the vector of cartesian forces, \(\dot{x}\) and \(\ddot{x}\) are vectors fo cartesian velocities and accretions, \(\dot{q}\) is the vector of the joint velocities and \(\tau\) is the vector of joint torques.
Reachable space approximation of in the desired horizon of interest \(\Delta t_{h}\) using the convex polytope formulation:
\[P_x = \{\Delta x~ |~ \Delta{x} = JM^{-1}\tau \Delta t_{h}^2/2,\]\[{\tau}_{min} \leq \tau \leq {\tau}_{max},\]\[\dot{q}_{min} \leq M^{-1}\tau \Delta t_{h} \leq \dot{q}_{max},\]\[{q}_{min} \leq M^{-1}\tau \Delta t_{h}^2/2 \leq {q}_{max} \}\]Based on the paper:by Skuric, Antun, Vincent Padois, and David Daney.In: Human-Friendly Robotics 2022: HFR: 15th International Workshop on Human-Friendly Robotics. Cham: Springer International Publishing, 2023.See the full formulaiton in the api docs.
New 📢 : Reachable space non-linear approximation in the desired horizon of interest \(\Delta t_{h}\):
\[C_x = \{ x~ |~ x = f_{fk}(q_0 + \dot{q}\Delta t),\]\[\dot{q}_{min} \leq \dot{q} \leq \dot{q}_{max},\quad {q}_{min} \leq q_0 + \dot{q}\Delta t \leq {q}_{max} \}\]See an example of how its used in the tutorials.
Human musculoskeletal models capacity metrics
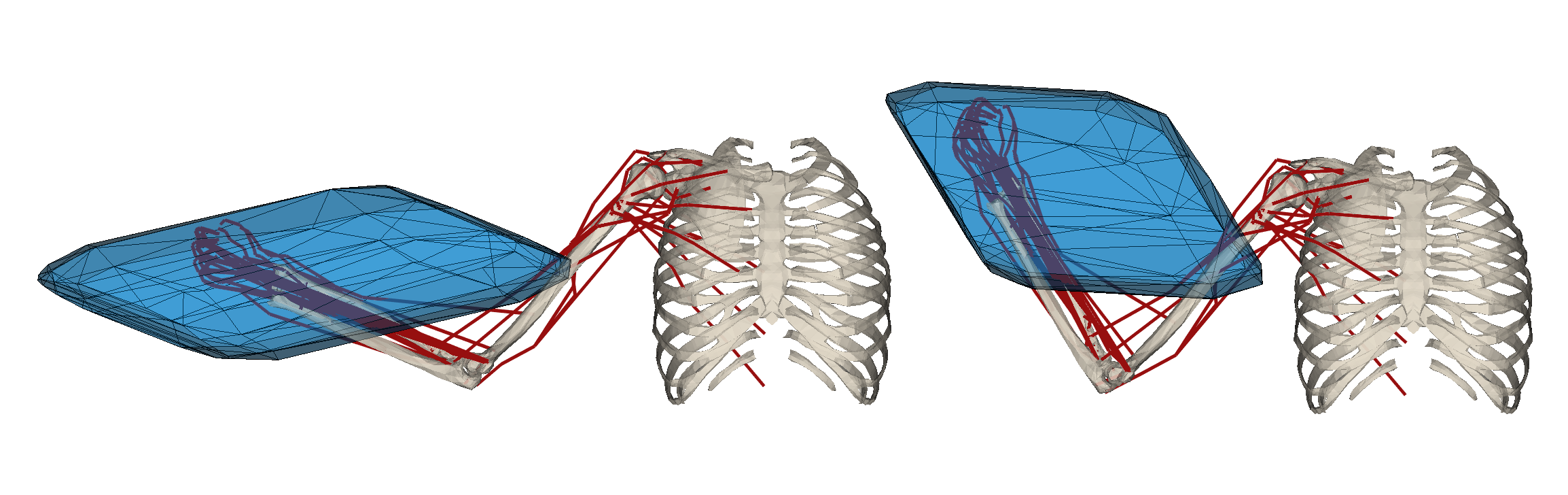
For the robotic manipulators the package integrates velocity, force and acceleration capacity calculation functions based on ellipsoids:
Velocity (manipulability) ellipsoid
\[E_v = \{\dot{x}~ |~ J\dot{q} = \dot{x},~ L\dot{q} = \dot{l} \quad ||W^{-1}\dot{l}|| \leq 1\}, \qquad W = diag(\dot{l}_{max})\]Acceleration (dynamic manipulability) ellipsoid
\[E_{a} = \{\ddot{x}~ |~ \ddot{x} = JM^{-1}NF, \quad ||W^{-1}F|| \leq 1\}, \qquad W = diag(F_{max})\]Force ellipsoid
\[E_{f} = \{f~ |~ NF = J^Tf,\quad ||W^{-1}F|| \leq 1\}, \qquad W = diag(F_{max})\]
And polytopes:
Velocity polytope
\[P_{v} = \{\dot{x} ~| \dot{l} = L\dot{q},~ \dot{x} = J\dot{q},~ \dot{l}_{min}\leq\dot{l}\leq\dot{l}_{max} \}\]Acceleration polytope
\[P_{a} = \{\ddot{x} ~| \ddot{x} = JM^{-1}NF,~ F_{min}\leq F\leq F_{max} \}\]Force polytope
\[P_{f} = \{f ~| J^Tf = NF,~ F_{min}\leq F\leq F_{max} \}\]
Where \(J\) is the model’s jacobian matrix, \(L\) si the muscle length jacobian matrix, \(N= -L^T\) is the moment arm matrix, \(f\) is the vector of cartesian forces, \($\dot{x}\) and \(\ddot{x}\) are vectors fo cartesian velocities and accretions, \(\dot{q}\) is the vector of the joint velocities, \(\tau\) is the vector of joint torques, \(\dot{l}\) is the vector of the muscle stretching velocities and \(F\) is the vector of muscular forces.
Performance evaluation of polytope metrics
The applicable methods to evaluate different polytope based metrics depend on the family of problems they correspond to. Therefore this section brings the information about which algorithm is used for which polytope metric and provides a brief performance evaluation their execution times.
Polytope Metric |
Algorithm |
Problem type |
Execution time [ms] mean \(\pm\) std. (max) |
|---|---|---|---|
Velocity |
HPSM |
\(x=By,~ y \in [y_{min}, y_{max}]\) |
3.6 \(\pm\) 0.21 (5.7) |
Acceleration |
HPSM |
\(x=By,~ y \in [y_{min}, y_{max}]\) |
6.6 \(\pm\) 1.4 (14.2) |
Force |
VEPOLI \(\!^2\) |
\(Ax=b, ~ b \in [b_{min}, b_{max}]\) |
6.8 \(\pm\) 0.88 (16.4) |
Force intersection |
VEPOLI \(\!^2\) |
\(Ax=b,~ b \in [b_{min}, b_{max}]\) |
98.2 \(\pm\) 29.33 (165.8) |
Force sum |
VEPOLI \(\!^2\) |
\(Ax=b,~ b \in [b_{min}, b_{max}]\) |
17.1 \(\pm\) 3.4 (44.9) |
Reachable space |
ICHM |
\(x=By,~ y \in P_{y}\) |
30.5 \(\pm\) 6.6 (76.7) |
The average execution time is calculated using 7 dof Franka Emika panda robot, the model was used with pinocchio software.
All the experiments are run on a computer equipped with 1.90GHz Intel i7-8650U processor. The results are obtained using
the benchmarking script provided in the examples folder, script link.
In case of human musculoskeletal models the methods used are given in the table below.
Polytope Metric |
Algorithm |
Problem type |
Execution time [ms] mean \(\pm\) std. (max) |
|---|---|---|---|
Force |
ICHM |
\(Ax=By,~ y \in [y_{min}, y_{max}]\) |
186.8 \(\pm\) 45.6 (281.6) |
Acceleration |
HPSM or ICHM |
\(x=By,~ y \in [y_{min}, y_{max}]\) |
378.8 \(\pm\) 62.3 (643.7) |
Velocity |
ICHM |
\(x=By,~ y \in P_{y}\) |
223.1 \(\pm\) 60.4 (389.1) |
The average execution time was calculated using 50 muscle 7 dof musculoskeletal model introduced by Holzbaur, the model was used with biorbd biomechanics software.
The experiments are run on a computer equipped with 1.90GHz Intel i7-8650U processor. The results are obtained using the benchmarking script
provided in the examples folder, script link.
As these times can vary significantly depending on the complexity of the model used and the hardware it is run on,
the users are encouraged to run the benchmark scripts themselves to get the most accurate results.
This package provides several benchmarking scripts in the examples folder, see link for more
details: link.
Compatible libraries
The package is compatible with the following libraries:
Library |
Example |
|---|---|